An isolated node in an undirected graph is a node that has no neighbors.

Suppose a graph \(G = (V, E)\) is represented using an adjacency matrix. What is the best possible worst-case time complexity of an efficient algorithm for computing the number of isolated nodes in the graph? State your answer as a function of \(|V|\) and \(|E|\) using asymptotic notation.

Suppose a graph \(G = (V, E)\) is stored using an adjacency list representation in the variable adj_list. What is the time complexity of the below code?

for lst in adj_list:
    for u in lst:
        print(u)

Let \(A\) be the adjacency matrix of the graph shown below:

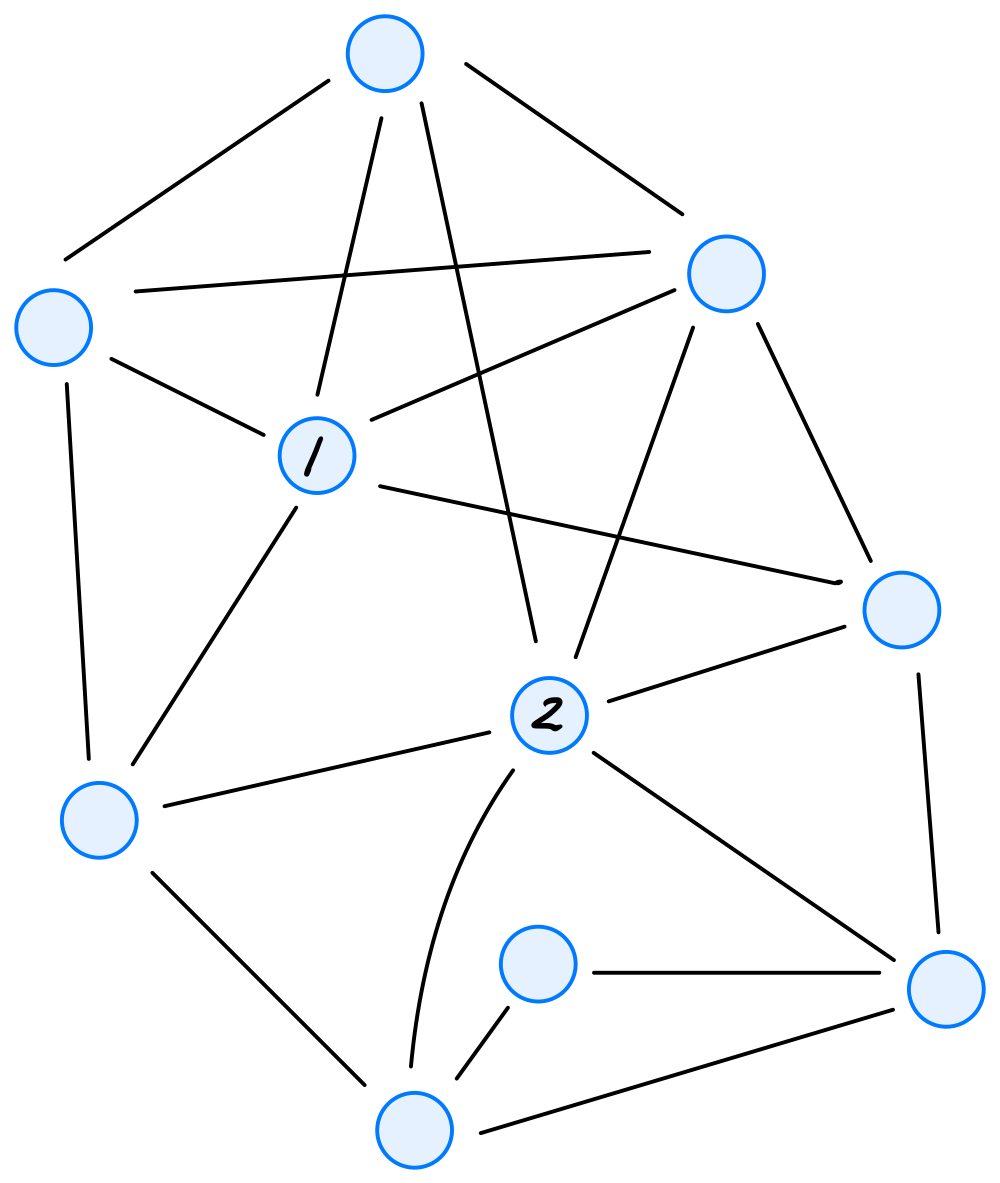
Let \(\vec{a}^{(1)}\) be the first row of \(A\) and \(\vec{a}^{(2)}\) be the second row of \(A\). What is \(\vec{a}^{(1)}\cdot\vec{a}^{(2)}\)? That is, what is the dot product between the first row of \(A\) and the second row of \(A\)? Your answer should be in the form of a number.

It may help to recall that the dot product between vectors \(\vec x = (x_1, \ldots, x_d)^T\) and \(\vec y = (y_1, \ldots, y_d)^T\) is equal to \(x_1 y_1 + x_2 y_2 + \ldots + x_d y_d\).

Let \(A\) be the adjacency matrix representing a directed graph with $n$ nodes. What is the greatest possible sum of any row of \(A\)?

An ``isolated node'' in a graph is a node that has no edges attached to it.

What is the worst case time complexity of an efficient algorithm that checks to see if a graph \(G = (V, E)\) has an isolated node? You should assume that the graph is represented as an adjacency list.